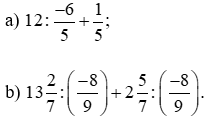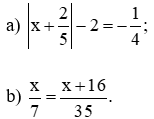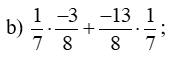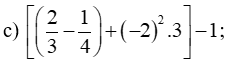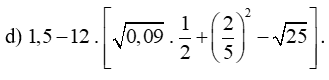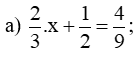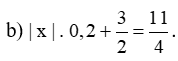Đề thi Học kì 1 - Kết nối tri thức
Năm học 2023 - 2024
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 1)
Bài 1. (1,5 điểm)
1. Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):
a)
b)
2. Tìm x, biết:
Bài 2. (0,75 điểm) Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 9 cm, chiều rộng là 6 cm. Tính độ dài đường chéo của hình chữ nhật (lấy kết quả với độ chính xác 0,005).
Bài 3. (3,0 điểm) Cho tam giác ABC có AB = AC, M là trung điểm của BC.
a) Chứng minh AMB = AMC.
b) Trên cạnh AB lấy điểm D. Từ D kẻ đường vuông góc với AM tại K và kéo dài cắt cạnh AC tại E. Chứng minh tam giác ADE cân.
c) Trên tia đối của tia ED lấy điểm F sao cho EF = MC, gọi H là trung điểm của EC. Chứng minh ba điểm M, H, F thẳng hàng.
Bài 4. (1,0 điểm) Bản tin dịch COVID-19 ngày 12/12/2021 của Bộ Y tế cho biết số ca mắc bệnh ở một số tỉnh/ thành phố như bảng sau:
| Số ca mắc COVID-19 ở một số tỉnh/ thành phố ngày 11/12/2021 | ||||
| Tỉnh/thành phố | Tp. Hồ Chí Minh | Tây Ninh | Đồng Tháp | Cần Thơ |
| Số ca mắc | 1 216 | 920 | 745 | 669 |
Hãy vẽ biểu đồ đoạn thẳng biểu diễn bảng thống kê trên.
Bài 5. (0,75 điểm) Một công ty phát triển kĩ thuật có một số thông báo rất hấp dẫn: Cần thuê một nhóm kĩ thuật viên hoàn thành một dự án trong vòng 17 ngày, công việc rất khó khăn nhưng tiền công cho dự án rất thú vị. Nhóm kĩ thuật viên được nhận làm dự án sẽ lựa chọn một trong hai phương án trả tiền công như sau:
– Phương án 1: Nhận một lần và nhận tiền công trước với mức tiền 170 triệu đồng;
– Phương án 2: Ngày đầu tiên nhận 3 đồng, ngày sau nhận gấp 3 lần ngày trước đó.
Em hãy giúp nhóm kỹ thuật viên lựa chọn phương án để nhận được nhiều tiền công hơn và giải thích tại sao chọn phương án đó.
ĐỀ SỐ 2
Bài 1. (1,5 điểm) Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):
Bài 2. (1,0 điểm) Tìm x, biết:
Bài 3. (1,5 điểm) Bạn Nam đi mua vở và nhẩm tính với số tiền hiện có thì chỉ mua được 10 quyển vở loại I hoặc 12 quyển vở loại II hoặc 15 quyển vở loại III. Biết rằng tổng giá trị tiền 1 quyển vở loại I và 2 quyển vở loại III nhiều hơn giá tiền 2 quyển vở loại II là 4 000 đồng. Tính giá tiền của mỗi quyển vở loại III.
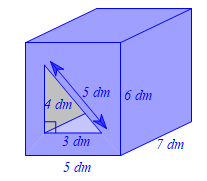
Bài 4. (1,0 điểm) Một khối gỗ hình lăng trụ đứng tứ giác có đáy là hình chữ nhật có kích thước là 5 dm, 6 dm và chiều cao 7 dm. Người ta khoét từ đáy một cái lỗ hình lăng trụ đứng tam giác, đáy là một tam giác vuông có hai cạnh góc vuông là 3 dm, 4 dm và cạnh huyền là 5 dm (hình vẽ).
Người ta cần sơn toàn bộ các mặt của khối gỗ, tính thể tích khối gỗ và diện tích bề mặt cần sơn.
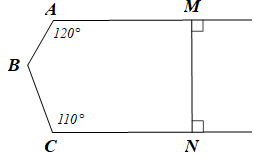
Bài 5. (1,0 điểm) Cho hình vẽ dưới đây.
a) Vẽ lại hình và viết giả thiết kết luận.
b) Chứng minh AM // CN.
c) Tính số đo góc ABC.
Bài 6. (1,0 điểm)
a) Một cửa hàng thời trang có chương trình giảm giá 20% cho tất cả các sản phẩm. Đặc biệt nếu khách hàng nào có Thẻ thành viên của cửa hàng thì được giảm giá thêm 10% trên giá đã giảm. Chị Phương đến cửa hàng mua một chiếc áo dạ, khi thanh toán hóa đơn, chị Phương chỉ cần trả 2 160 000 đồng do có thẻ thành viên. Hỏi giá niêm yết của chiếc áo là bao nhiêu?
b) Tìm giá trị lớn nhất của biểu thức
Câu 1 (2đ) Thực hiện phép tính:
a) (−0,25) . 40 + 3;
Câu 2 (1đ):Tìm x, biết:
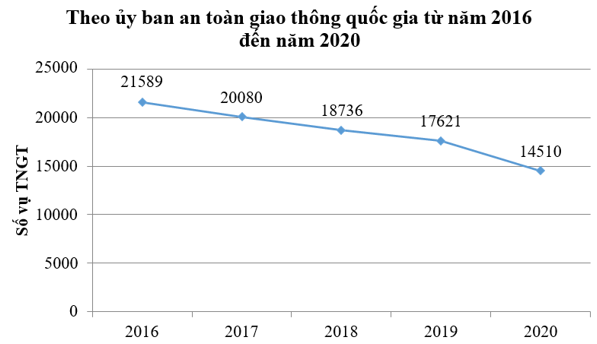
Câu 3 (1đ): Cho biểu đồ đoạn thẳng biểu diễn số vụ tai nạn giao thông cả nước tính từ năm 2016 đến năm 2020.
Em hãy chobiết sốvụ tai nạn giao thông của năm 2019 so với năm 2018 giảm bao nhiêu phầntrăm và năm 2020 so với năm2019 giảm bao nhiêu phần trăm, năm nào giảm sâu hơn?
Câu4 (1đ): Áp dụng quy tắc làm tròn số để ước lượng kết quả của mỗi phép tính sau :
a) (–74,17) + (– 75,83) ;
b) (– 20,041) . 49,815.
Câu 5 (1đ): Cho ∆ABC có
a) Tính
b) Chứng minh rằng AB // Cy.
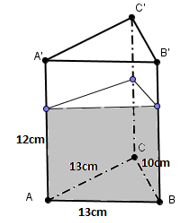
Câu 6 (1đ): Một bình thủy tinh hình lăng trụ đứng ABC.A’B’C’ , đáy là tam giác cân ABC có kích thước như hình vẽ. Mực nước hiện tại trong bình bằng